Lumps: Shape Model directly from Mesh
What is the Use Case?
The lumps use case demonstrates a minimal example of running ShapeWorks directly on a mesh using a synthetic dataset. The shapes in this dataset are spheres with two lumps or nodes that vary in size. The use case demonstrates that the ShapeWorks workflow results in a correct shape model- i.e., only the position of particles on the lumps vary; the rest are constant across the shape population.
Grooming Steps
This is a synthetic dataset that is already in alignment and does not require grooming.
Here are some examples of the meshes:
Relevant Arguments
--use_subsample --num_subsample --use_single_scale --tiny_test
Optimization Parameters
The python code for the use case calls the optimize command of ShapeWorks which reads the project sheet with the shape filenames and optimization parameter values. See Project excel file for details regarding creating the project sheet.
Below are the default optimization parameters for this use case.
{
"number_of_particles": 512,
"use_normals": 0,
"normals_strength": 10.0,
"checkpointing_interval": 100,
"keep_checkpoints": 0,
"iterations_per_split": 2000,
"optimization_iterations": 500,
"starting_regularization": 10,
"ending_regularization": 1,
"recompute_regularization_interval": 1,
"domains_per_shape": 1,
"relative_weighting": 10,
"initial_relative_weighting": 1,
"procrustes_interval": 0,
"procrustes_scaling": 0,
"save_init_splits": 0,
"verbosity": 0
}
Analyzing Shape Model
Here is the mean shape of the optimized shape mode using single-scale optimization. Note the two tiny lumps at the top, and towards the right.
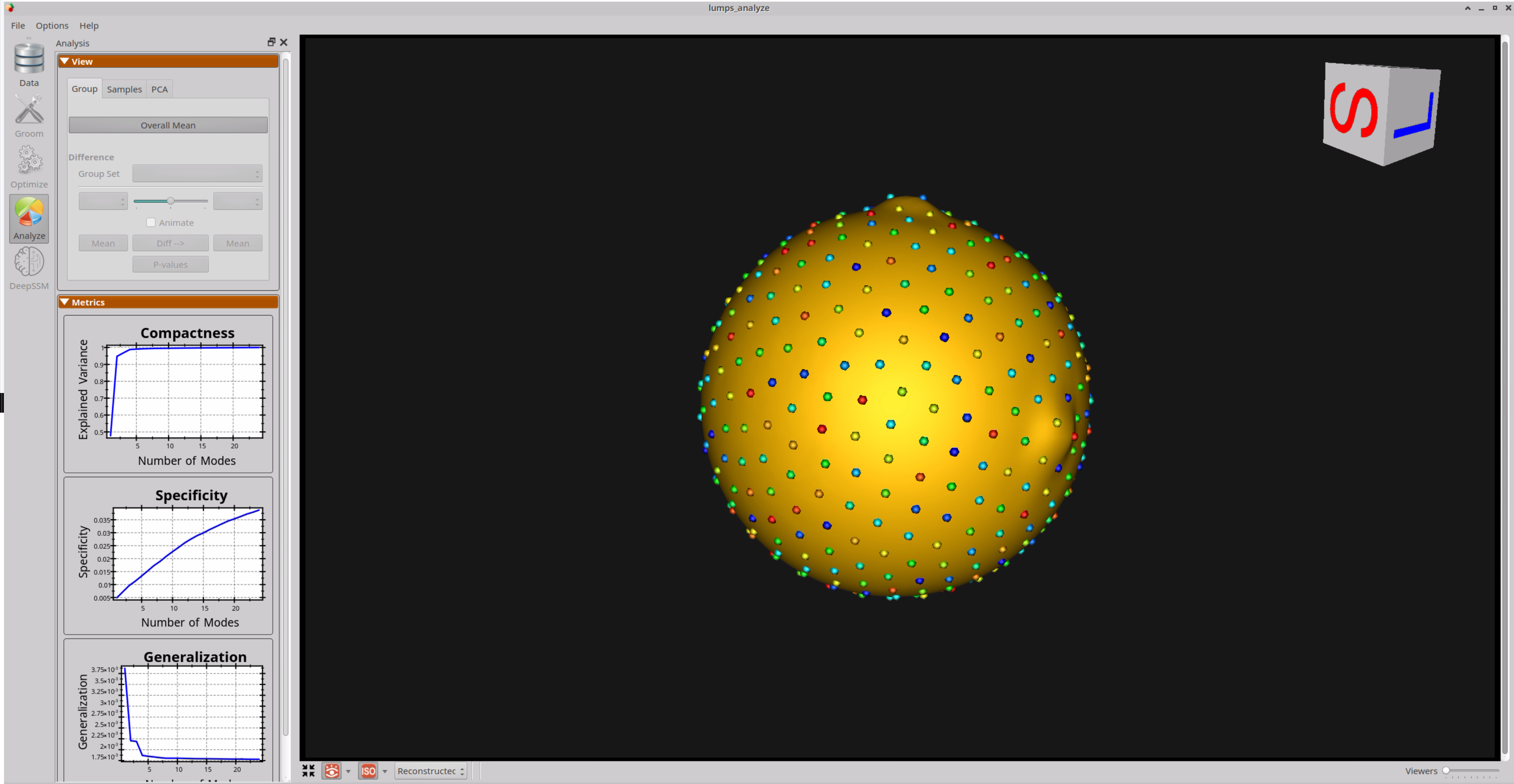
Here are lumps samples with their optimized correspondences.

Here is a video showing the shape modes of variation (computed using principal component analysis - PCA) of the lumps dataset using single-scale optimization.
Note that the particles which do not lie on the lumps remain stationary. The shape model correctly caputures the modes of variation.