Shape Model for Multiple Domains from Segmentations
What is the Use Case?
The ellipsoid_multiple_domain use case demonstrates using ShapeWorks tools to perform shape modelings for anatomies with multiple structures (domains), e.g., joints, to capture inter-domains correlations and interactions.
The dataset available for this use case:
- ellipsoid_joint_rotation - two stacked ellipsoids with the same radii, with the top ellipsoid rotating w.r.t the bottom ellipsoid.
Grooming Steps
This is how the segmentations in the dataset look before grooming.Here it can been seen that the ellipsoids have random centers andn orientations.
- Isotropic Resampling: Binary segmentations in the ellipsoid joint dataset are resampled with an isotropic voxel spacing.
- Reference Selection: For the ellipsoid_joint datasets available on the ShapeWorks portal, the mode of variation is rotation and/or size of the second ellipsoid w.r.t to the first ellipsoid. Hence, we align the shapes using the first domain as the reference. This is domain-specific alignment. The reference is selected by first computing the mean (average) distance transform of the segmentations belonging to the reference domain, then selecting the sample closest to that mean (i.e., medoid).
- Rigid Alignment: For all the shapes, the transformation is calculated to factor out translation and rotation based on the reference shape.This transformation matrix will be sent to the optimizer as a 'prefix transform' 4.Bounding Box: The smallest region which fits all of the samples is found.
- Cropping: The segmentations are cropped to the size of the bounding box.
- Padding: The segmentations are padded with zeros on every side.
- Distance Transform: Finally, the smooth signed distance transform is computed, and the dataset is now ready for the optimize phase.
Distance transform obtained after grooming.Here we show how the shapes would look like if the transforms are applied.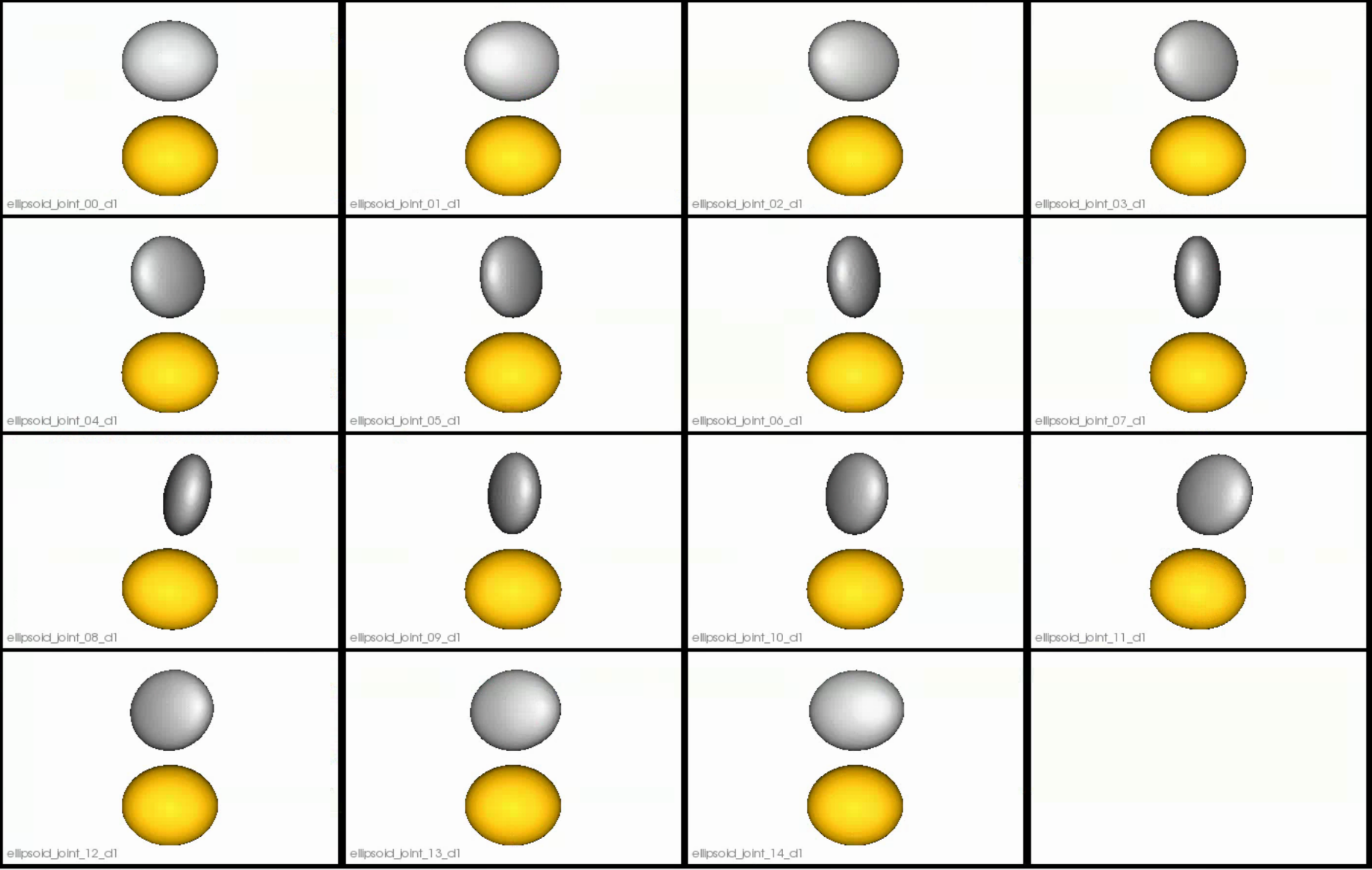
Relevant Arguments
--use_subsample --num_subsample --use_single_scale --mesh_mode --tiny_test
Optimization Parameters
The python code for the use case calls the optimize command of ShapeWorks which reads the project sheet with the shape filenames and optimization parameter values. See Project excel file for details regarding creating the project sheet.
Below are the default optimization parameters for this use case.
{
"checkpointing_interval" : 200,
"keep_checkpoints" : 0,
"iterations_per_split" : 200,
"optimization_iterations" : 200,
"starting_regularization" :1000,
"ending_regularization" : 0.1,
"recompute_regularization_interval" : 1,
"domains_per_shape" : domains_per_shape,
"relative_weighting" : 10,
"initial_relative_weighting" : 0.1,
"procrustes_interval" : 0,
"procrustes_scaling" : 0,
"save_init_splits" : 0,
"verbosity" : 0
}
num_particles = [128,128]
Analyzing Shape Model
Once the python code runs the optimization, the files are saved in the Output folder after which ShapeWorks Studio is launched from the python code to analyze the model.
Here is the optimized shape.
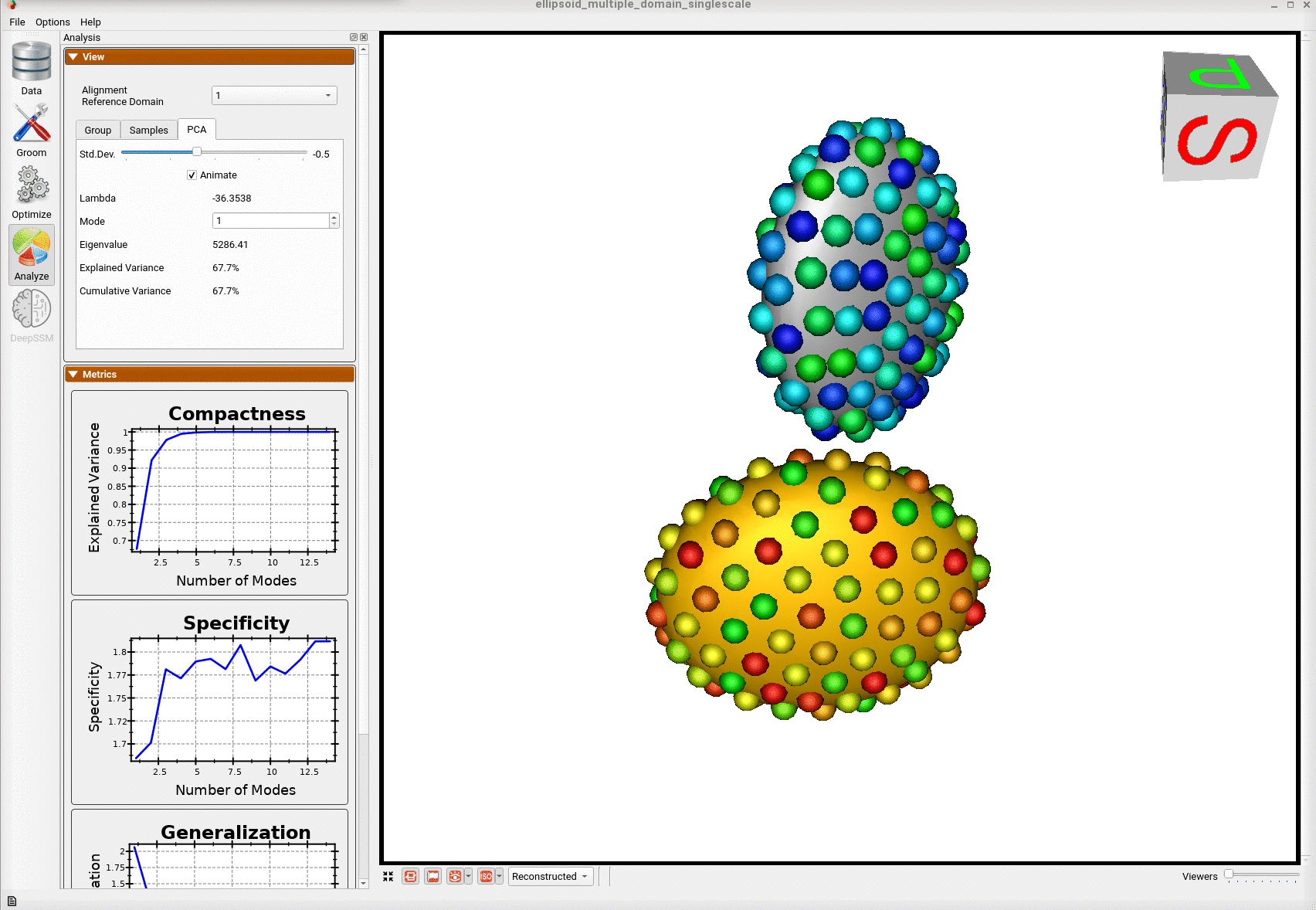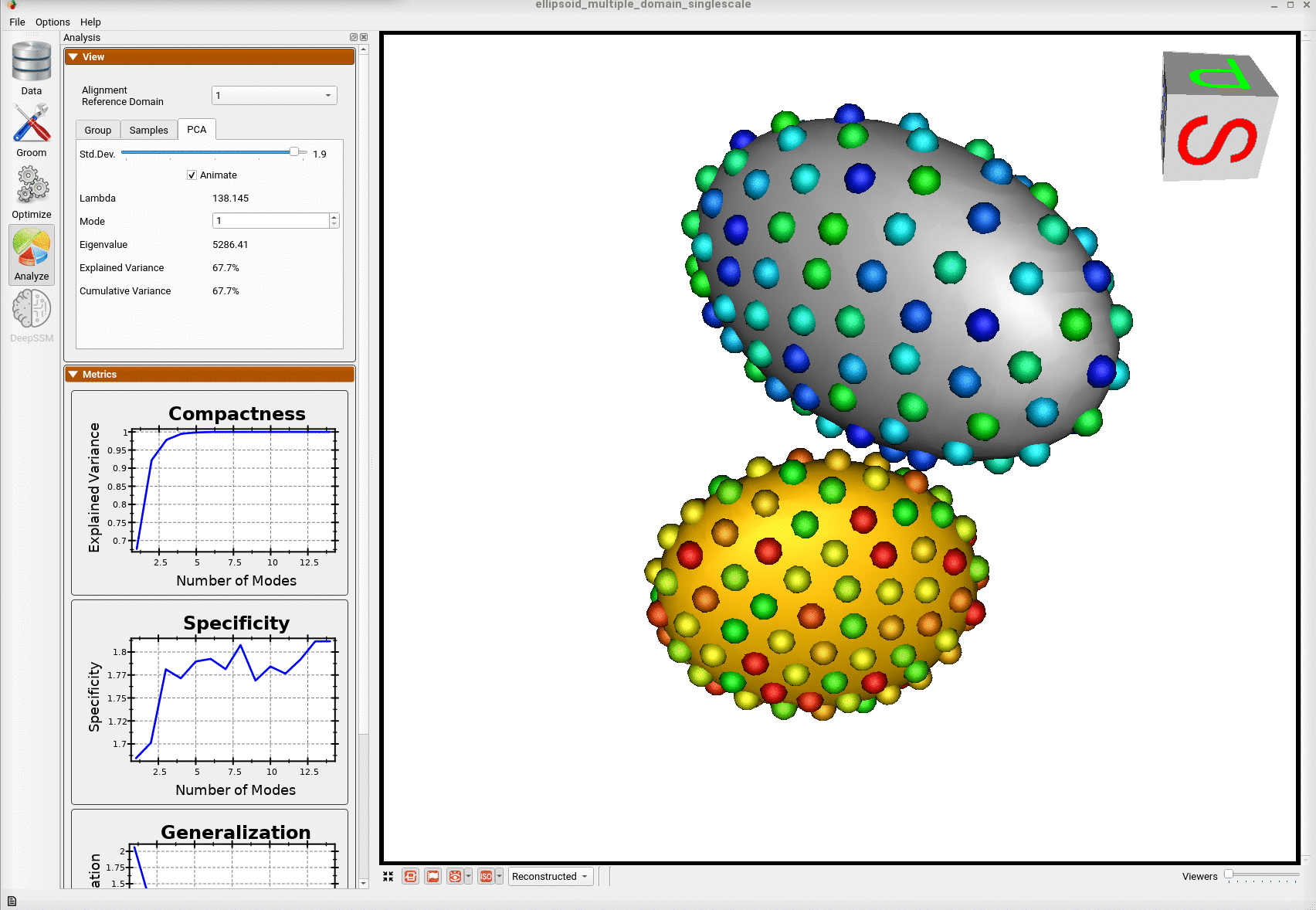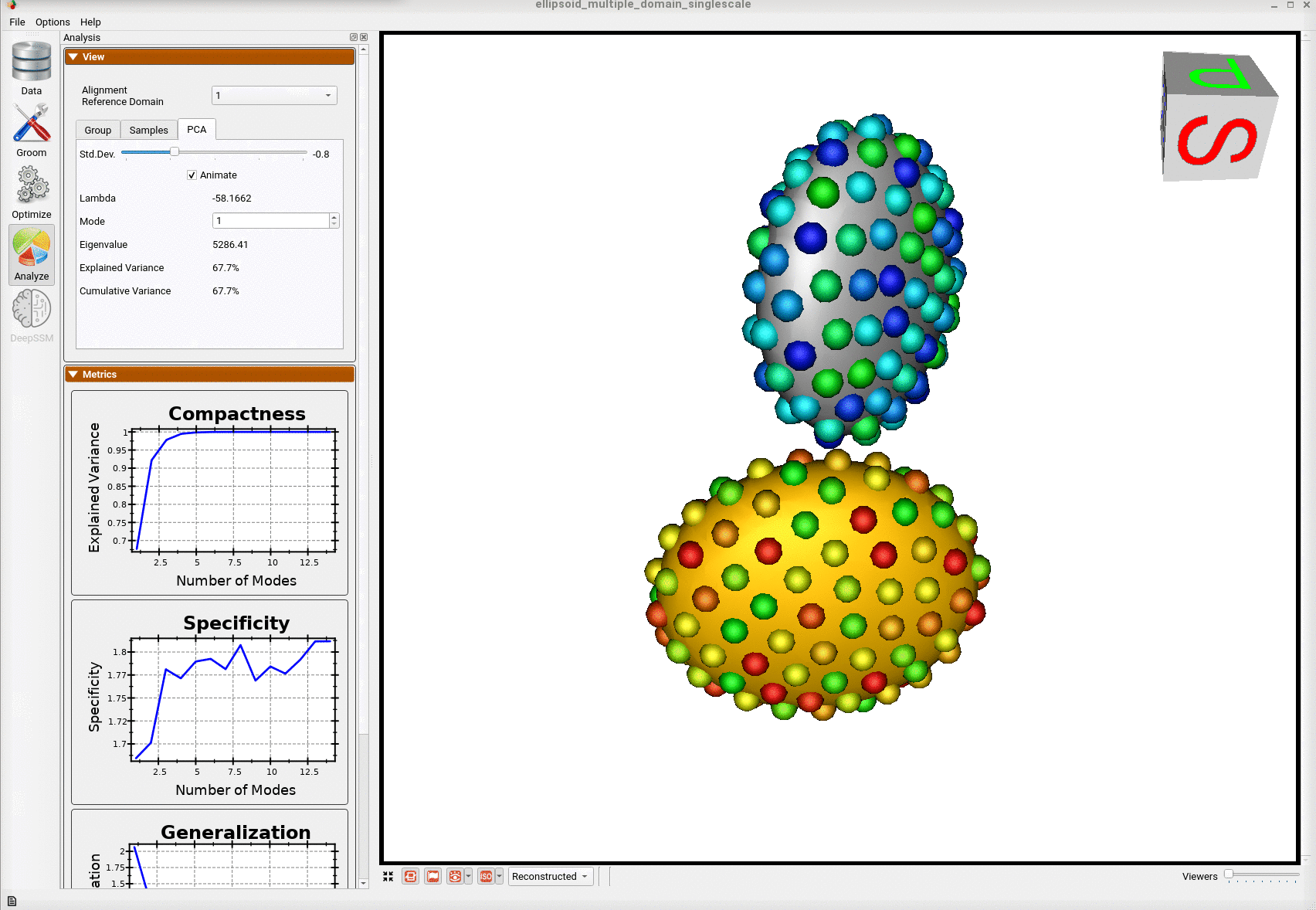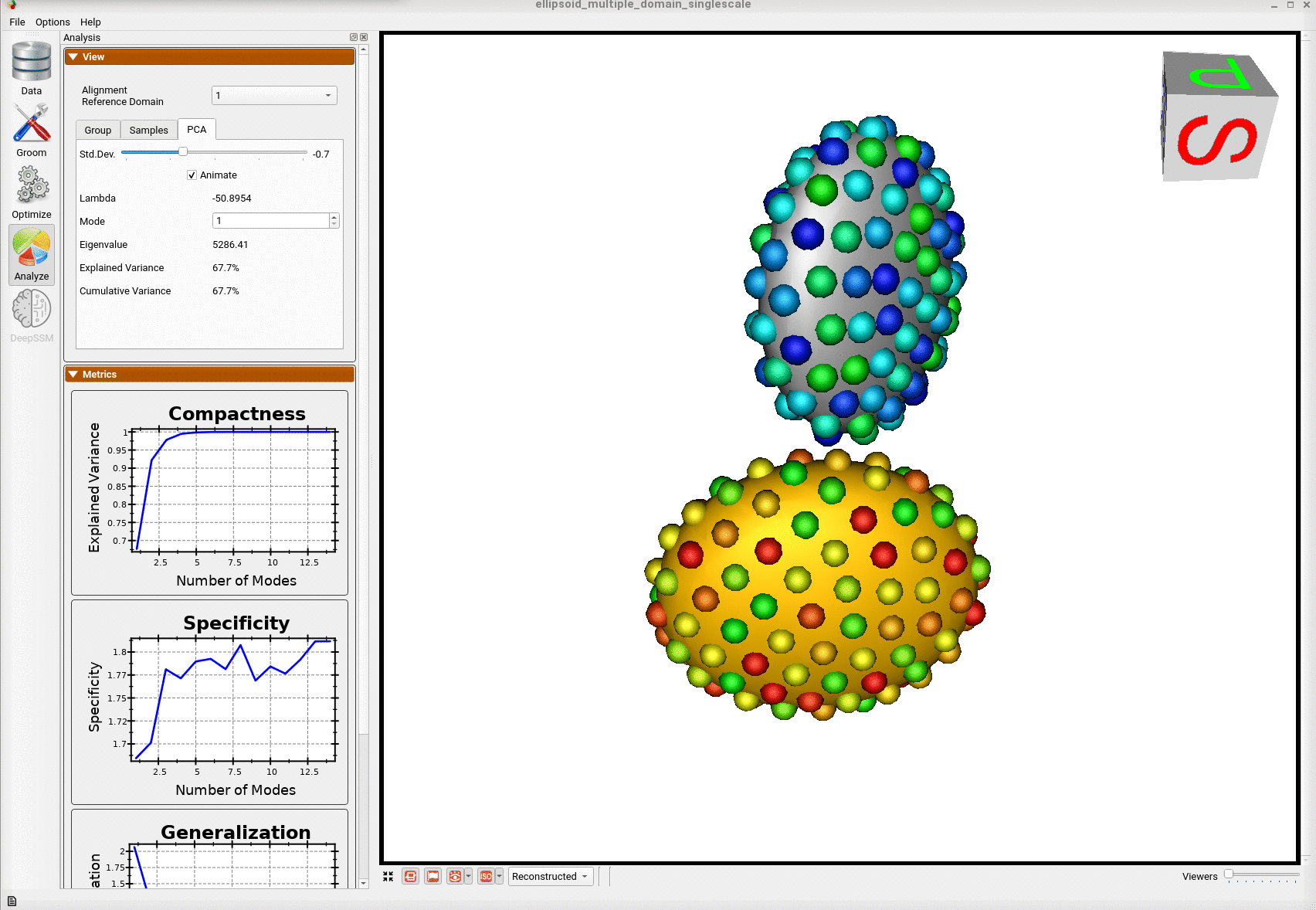
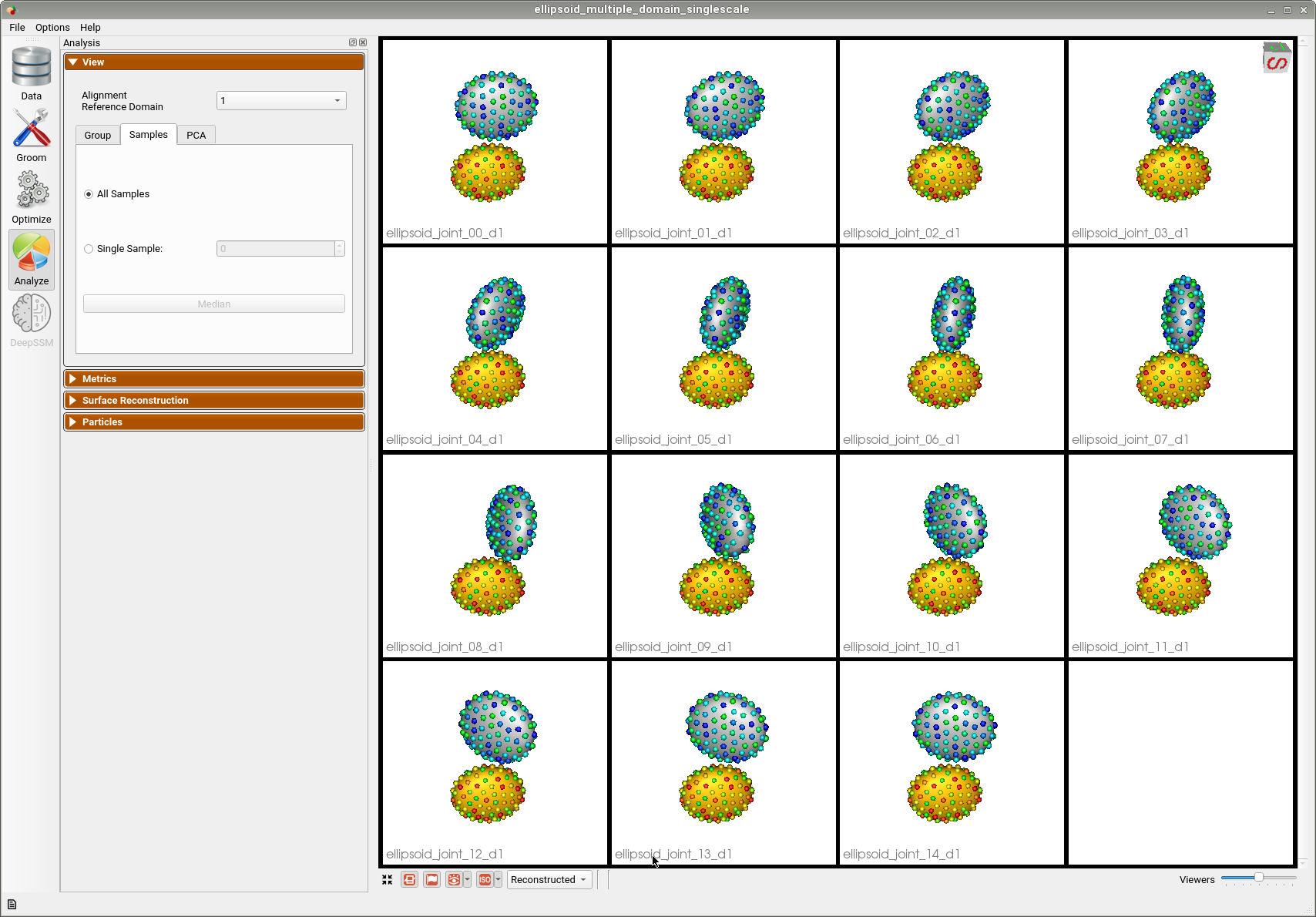
Below are the particles for each sample; we can see they are uniformly distributed.